
0. 메타데이터 확인
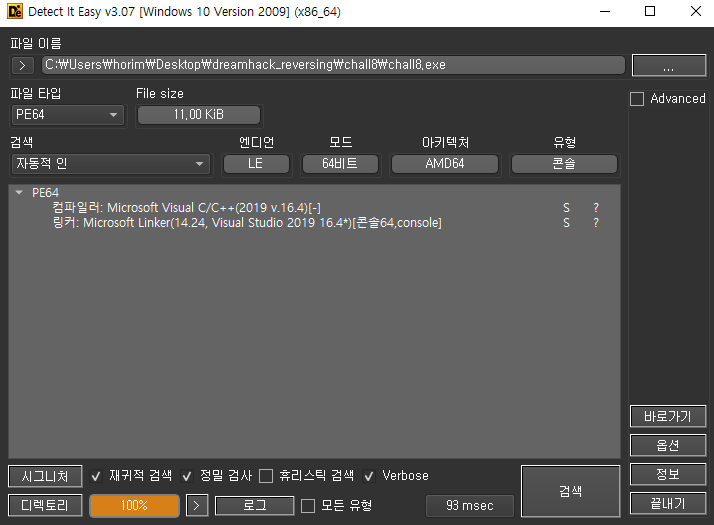
PE64, C언어로 작성된 프로그램
1. 동적 분석
Input 나오고, 사용자 입력 받고, Correct / Wrong 판별해 보여줌
콘솔에서 stdin 받음
2. 정적 분석
역시나 똑같음
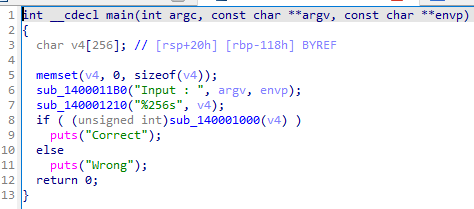
이제 sub_140001000을 들여다보자.
2.1. sub_140001000
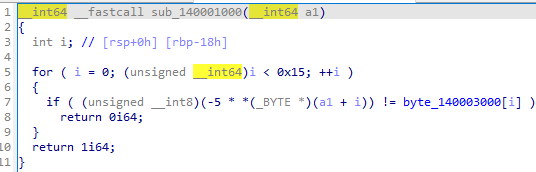
안예뻐
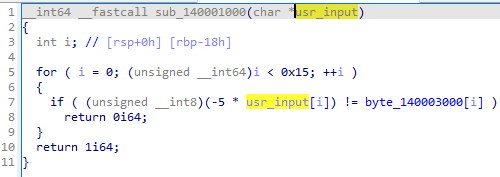
이젠예뻐
byte_140003000 안에 담긴 데이터는 아래와 같음
AC F3 0C 25 A3 10 B7 25 16 C6 B7 BC 07 25 02 D5 C6 11 07 C5
궁금한 점. 왜 -5를 곱한 걸까? 이 문제의 의도가 뭘까?
1byte 자료형이 마이너스를 표현하는 방법에 대해 알아보라는 뜻 아닐까?
흠… 진짜 왜지?
2.2. 2’s complement
이진수의 모든 자리 숫자를 반전시키고, 1을 더해서 2의 보수를 구한다.
2의 보수인 수는 원래 숫자의 음수로 취급된다.
(자세한 건 생략)
2.3. sub_140001000 내부 비교 루틴(어셈블리)
for ( i = 0; (unsigned __int64)i < 0x15; ++i ) { if ( (unsigned __int8)(-5 * usr_input[i]) != byte_140003000[i] ) return 0i64; }
뭔가 감이 안 오는 것 같으면 어셈을 한 번 보는 것도 좋으니, 어셈으로 위 비교문의 if 조건을 보자.
movsxd rax, [rsp+18h+var_18]mov rcx, [rsp+18h+arg_0]movzx eax, byte ptr [rcx+rax]imul eax, 11111011band eax, 11111111bmovsxd rcx, [rsp+18h+var_18]lea rdx, byte_140003000
movzx ecx, byte ptr [rdx+rcx]cmp eax, ecxjz short loc_140001053
imul~and 까지가 가장 중요한 부분이다.
앞서 설명한 2’s complement를 감안할 때, imul 의 operand 2는
0x11111011(2) == -0x00000101(2) == -5(10)
and 연산의 이유는 뭐지?
아 r계열 레지스터(64bit) 에 e계열 레지스터인 것처럼 값을 넣었으니까(32bit) 상위 32bit의 값을 정리해 주려고 하는 거구나
- 5 곱하는 이유…char 자료형이니 8bit 내에서 일어나는 일을 보고 싶은 것 같은데
이걸 어떻게 표현해야 하지?
imul이라는 레지스터가 중요함. 이건 부호 연산을 할 수 있는 레지스터임 → 이걸 썼다는 것은 음수를 썼을 가능성이 높다는 뜻
동적 분석은 보통 x64dbg 사용한다
연산하고 and 연산이 추가되는 경우는, 하위 n 비트를 구하기 위한 목적이 크다. 형변환이라든가… 자료형(크기) 다른 포맷으로 변경한다든가….
2.3. 난관에 봉착하다
- 5*usr_input == 정답배열이어야 하는데
이걸 뒤집으면
5 * usr_input == -정답배열
즉, 정답배열에 2’s complement를 취한 걸 정답’ 라고 하면
뭘 5번 덧셈해야(ALU는 덧셈연산밖에 못하니까) 정답’ 이 되는지 나와야 하는데, 안 나온다.
심지어 usr_input은 char type라서 1byte짜리로, 부동소수점 타입도 안 된다.
2.4. 난관에서 빠져나왔다
어차피 1byte짜리니까, 0~255까지 모든 숫자를 넣어보면서,
- 5*usr_input == 정답배열을 충족하는 0x15짜리 길이 문자열을 도출해도 된다고 생각했다.
브루트포싱은 아래와 같이 했음
tmp=['AC F3 0C 25 A3 10 B7 25 16 C6 B7 BC 07 25 02 D5 C6 11 07 C5']
tmp2=tmp[0].split(' ')
byte_140003000=[]
solve=[]
for i in tmp2:
byte_140003000.append(int(i, 16))
for i in byte_140003000:
solve.extend(brute_force for brute_force in range(0, 256) if ((brute_force*0xFB)&0xFF == i & 0xFF))
print(solve)
solve_tmp=[chr(i) for i in solve]
solve_string=[]
solve_string.append(''.join(solve_tmp))
print(solve_string)
플래그 획득까지 완료
3. 질문.
그런데 왜 역산이 불가능하지?
개인적으로 추측해 보았다.
1byte로 표현하는 수라면, 0~255 까지를 한 주기로 하는 정수의 모듈러 군이다.
모듈러 군 내에서 곱셈은 일대일 함수가 아니므로 곱셈과 나눗셈의 역산 관계가 성립되지 않는다. 하나의 역원 존재 불가
곱셈이고 나눗셈이고 덧셈의 연장인데 왜? 라고 생각할 수 있을 것 같다. 그러나 모듈러 연산이 적용되는 닫힌군이라는 게 이 역산 불가의 원인으로 작용하므로… 음수는 의미없고
이런 원리를 이용한 게 PKI이고.
즉 밑을 상대적으로 작게(255) 들고 가는 모듈러 집합이라 5라는 작은 수를 곱해도 80% 이상 확률로(해당 군의 약 20%인 0~50까지는 5를 곱해도 255 이상이 아님) 나머지 연산이 이루어질 수 있기 때문에 어쩔 수 없이 (1-0.8^0x14) * 100 == 98.845% 의 확률로 복원 불가능한 정보임
따라서 브루트 포싱만이 답이라고 생각함.
